Pictures to Make Maths Easy the Sum of 13

12 Math Tricks to Help You Solve Problems Without a Calculator

Working it out in your head

Addition + Subtraction

1. Addition

The first trick is to simplify your problem by breaking it into smaller pieces. For example, we can rewrite

          567 + 432            
= 567 + (400 + 30 + 2)
= 967 + 30 + 2            
= 997 + 2            
=            999

Switch

It's often easier to work with adding a smaller number, so instead of 131 + 858, swap the numbers

          858 + 131            
= 858 + 100 + 30 + 1            
=            989

2. Subtraction

Using the complement of a number can help make subtraction easier. The complement is the difference between the original number and a round number — say 100, 1000.

Here are some examples with the number and its complement compared with 100:

          67:33, 45:55, 89:11, 3:97

Notice that the second digits add up to 10, and the first digit adds up to 9.

Here is how this is helpful

          721–387            
# the complement of 87 is 13, so we can swap 387 with 400 – 13
-> 721 — (400 - 13)            
= 321 - -13            
= 321 + 13
=            334

Another method is to write out the larger number so it ends in 99. With the same example:

          721 -> (699 + 22)
= 699 – 387 + 22            
= 312 + 22            
=            334

Multiplication

3. Elevens

For a two-digit number, add the digits and put the answer in the middle of the number you are multiplying:

If the sum is greater than 10, add the tens digit to the next column to the left, and write the ones digit in the answer. For example, 4+8 = 12, write down 2 and carry the 1 into the next column.

          48 x 11            
-> 4_8            
-> 4+8 = 12            
-> 4,12,8            
->            528

The process is a little more complicated for three-digit and greater numbers, but it works in a similar way. This time keep the first and last digit and sum the digits in pairs

          725 X 11            
-> 7__5            
-> 7_,(7+2=9), (2+5=7), _5            
->            7975                    51973 x 11            
-> 5__3            
-> 5_,(5+1=6),(1+9=10), (9+7=16), (7+3=10), _3            
# where the sum is greater than ten we move the tens digit into the next column            
-> 5,(6+1),(0+1),(6+1),(0),3            
->            571703

4. Nines

Multiplying by nines can be simplified by multiplying by 10 and subtracting the original number

          799 x 9            
= 799 x (10 -1)            
= 7990 – 799            
=            7191

Use the same method for anything ending in 9

          72 x 89            
= 72 x (90–1)            
= (70 x 90) + (2 x 90) — 72            
= 6300 + 180–72            
=            6408

5. How to solve squares

You can re-write a square equation into numbers that are easier to deal with using this formula

          n^2 = (n+d)(n-d) + d^2

where n is the number to be squared, and d is the difference

Here's an example

          57^2            
= (57+3)(57–3) + 3^2
# we add 3 to 57, as 60 is easier to multiply than 57, and subtract 3 from the second 57
-> 60 x 54 + 9            
= 3000 + 240 + 9            
=            3249

The ultimate example is when you are squaring a number ending in 5, then round one number up to the nearest 10, the other number down to the nearest 10, and add 25.

          65^2            
= (60 x 70) + 5^2            
= 4200 + 25            
=            4225

6. Close together method

A similar method works for multiplying numbers that are close together. The formula works for all numbers, but it doesn't simplify well unless the numbers are similar.

Here's the formula. n is the "base" number

          (n+a)(n+b) = n(n + a + b) + ab

An example:

          47 x 43            
= (40 + 7)(40 + 3)            
= 40 x (40 + 3 + 7) + (7 x 3)
= (40 x 50) + (7 x 3)            
= 2000 + 21            
=            2021

In this example, the ones digits add up to ten, so our "base" number and the multiplier are round numbers (40 and 50).

Here's another example. Reduce the smaller number to reach the nearest round number — our base number, in this case, 40. Add the difference to the larger number. Multiple the base and larger number. Finally, add the product of the difference between the original numbers and the base number.

          47 x 42            
= (40 + 7) x (40 + 2)            
= (40 + 7 + 2) x 40 + (7 x 2)
= (49 x 40) + (7 x 2)            
= (40 x 40) + (40 x 9) + (7 x 2)
= 1600 + 360 + 14            
=            1974

You can also round up to the base number. As the original numbers are smaller than the base, we add the product of two negative numbers.

          47 x 42            
= (50 x 39) + (-3 x -8)            
= (50 x 30) + (50 x 9) + (-3 x -8)
= 1500 + 450 + 24            
=            1974

This works for three-digit numbers too. In this case, the base number is between our numbers, so the product is a negative number.

          497 x 504            
= (500 – 3) x (500 + 4)
= (500) x (500 + 4 - 3) + (-3 x 4)
= 500 x 501 - 12
= 250,000 + 500 – 12
=            250,488

Division

7. Simplify Calculations

You can simplify some equations before you even start. For example, divide both the divisor and dividend by two.

          898 / 4            
= 449 / 2            
= 224 and ½

Note with this method, you have to write the remainder as a fraction:

          898/4 has a remainder of 2 — divided by 4
449/2 has a remainder of 1 — divided by 2

The fraction is the same, but the absolute number is different.

When dividing by 5, modify the equation by multiplying by 2. It is much easier to divide by 10. For example:

          1753/5            
= 3506 / 10
=            350.6

8. Test for Divisibility

There are many ways to quickly whether a number is a factor.

2: The number is even.

          Example 28790 is even, so it is divisible by 2.

3: The sum of the digits is divisible by 3.

          Example: 1281 -> 1+2+8+1 = 12            
-> 12 is a multiple of 3, so 1281 is divisible by 3

4: The last two digits are divisible by 4. Why does this work? 100 is a multiple of 4, so we only have to check the last two digits.

          Example: 1472, 72 is divisible by 4, so 1472 is divisible by 4.

5: The number ends in 5 or 0.

          Example: 575 ends in 5, so it is divisible by zero

6: The number is even, and the sum of the digits is divisible by 3. 6 is 3 x 2, so the rules of 2 and 3 apply.

          Example: 774 is even and 7+7+4 = 18            
-> 18 is divisible by 3, so 774 is divisible by 6.

7: Add or subtract a multiple of 7 to your number so that it ends in zero. Drop the last digit with the zero and repeat the process. Continue until you can determine whether the result is divisible by 7.

          Example: 2702 add 98 (7 x 14) -> 2800, drop the zeroes
-> 28 is a multiple of 7, so 2702 is divisible by 7.

8: The last three digits are divisible by 8.

          Example: 79256, 256 is divisible by 8, so 79256 is divisible by 8.          (Alternate rule: if the hundreds digit is            even, last            2            digits divisble by 8, if hundreds digit is            odd, last            2            digits            + 4            divisible by 8)

9: The same rule as 3, but with 9. If the sum of the digits is divisible by 9, then the number is divisible by 9.

          Example: 13671 -> 1+3+6+7+1 = 18            
-> 18 is divisible by 9, so 13671 is divisible by 9

10: The number ends in 0.

          Example: 280 ends in 0, 280 is divisible by 10

11: Similar rule to 3 and 9, start at the right digit and alternate subtracting and adding the remaining digits. If the answer is zero, or a multiple of 11, then the number is divisible by 11.

          Example: 12727 -> 1 - 2 + 7 - 2 + 7 = 11, so 12727 is divisible by 11.

You can check out some additional methods here.

9. Dividing large numbers by 9

          Example:
-> 10520/9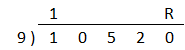

Write the first digit above the equation and write an "R" (for remainder) above the last digit. Add the number you just wrote and the number diagonally below and to the right of it. Write this new number in the second spot. Add that number to the number diagonally below and to the right. Continue this process until you reach the R.

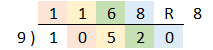
Sum the numbers with the same color to create the next digit

Finally, add the last digit to the number below the R to get your remainder.

          10520/9
=            1168 R8            
or 1168.889

Here's another example:

          -> 57423/9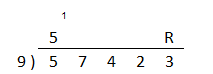

This time after we've completed the first step, the sum of our first number and the number diagonally below and to the right is larger than ten (5+7 =12). We put a one above the first digit and subtract nine from it. (We are dividing by a base of nine, so we subtract nine rather than ten). Place the resulting number in the second position (12–9 = 3). Continue with the same process.

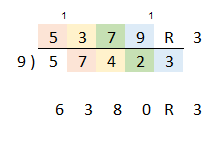
In this example, our remainder is larger than 9 (9+3 = 12). Once again, we carry a one above the previous digit and subtract nine from the remainder, leaving us with three. Now add the result and the carry digits.

          57423 / 9            
=            6380 R3
            or 6380.333

Percentages and Fractions

10. Reverse the question

Percentages are associative, so sometimes reversing the question's order makes it easier to calculate.

          Example:            
What's 36% of 25            
-> is the same as 25% of 36            
-> 25% is ¼            
-> 36/4 = 9            
36% of 25 is            9

11. Fractions

As you can see with the use of ¼ in the last example, it helps know fractions and how they relate to percentages.

          1/2 = 50%          1/3 = 33.33%, 2/3 = 66.67%,          1/4 = 25%, 3/4= 75%          1/5 = 20%, 2/5 = 40% …          1/6 = 16.67%, 5/6 = 83.33% (2/6 = 1/3, 3/6 = 1/2, 4/6 = 2/3)          1/7 = 14.2857%, 2/7 = 28.5714%, 3/7 = 42.8571%, 4/7 = 57.1428%  (note the recurring .142857 pattern)          1/8 = 12.5%, 3/8 = 37.5%, 5/8 = 62.5%, 7/8 = 87.5%          1/9 = 11.11%, 2/9 = 22.22%, 3/9 = 33.33% …          1/10 = 10%, 2/10 = 20% …          1/11 = 9.09%, 2/11 = 18.18%, 3/11 = 27.27% …          1/12 = 8.33%, 5/12 = 41.67%, 7/12 = 58.33%, 11/12 = 91.67%

12. Rule of 72

The rule of 72 provides an estimate of how many years it will take an investment to double in value at a given percentage return. It works by dividing 72 by the percentage, with the answer as the number of years it will take to double.

          2% -> 72/2 = 36, approximately 36 years to double
8% -> 72/8 = 9, approximately 9 years to double

Note that the rule of 72 is a guideline based on the natural log of 2 — which gives 0.693. So a rule of 69.3 would be more accurate, but 72 is easier to calculate.

There is also a rule of 114 for tripling an investment and a rule of 144 for quadrupling your money.

Additional Resources

I found two books by Arthur Benjamin to be helpful on this topic. Many of the examples in this blog were inspired by these books. You can check them out here.

https://www.amazon.com/Secrets-Mental-Math-Mathemagicians-Calculation/dp/0307338401/

Please leave a comment if you found this helpful, or share any other useful tricks you have come across.

vargasprocke.blogspot.com

Source: https://towardsdatascience.com/12-math-tricks-to-help-you-solve-problems-without-a-calculator-704fdd663286